设计准备

所需工具

MATLAB 2021b ; solidworks 2021 ; TracePro;

设计要求

设计一个能够将5毫米大小的LED光源发出的光照射到两米外，形成直径为3米的光斑的配光器。该配光器的工作面为旋转抛物面。根据光路可逆原理，该配光器的设计与集光器的原理类似。

设计原理

边光原理

原理：若一个具有一定光展的光源发出的光线经过一个或几个序列化的单调正则光学表面的光学作用后投向目标面形成光斑，则整个光学过程具有以下两个性质：一是光源的边光成为光斑的边光；二是光源的内光映射为光斑的内光，并保持光线的拓扑结构不变。

根据边光原理，在设计集光器的外形尺寸时，只需要考虑边光，进而可以简化设计的难度。

抛物线的性质

抛物线上的点到焦点的距离等于抛物线上的点到准线的距离相等。如果我们假设太阳光以基本上平行的光线到达表面，并应用斯涅尔定律（反射角等于入射角），我们可以将焦点指定为接收器的理想位置。

抛物线标准方程的表达式 \[ y^2=4f\_x \]

配光器的设计

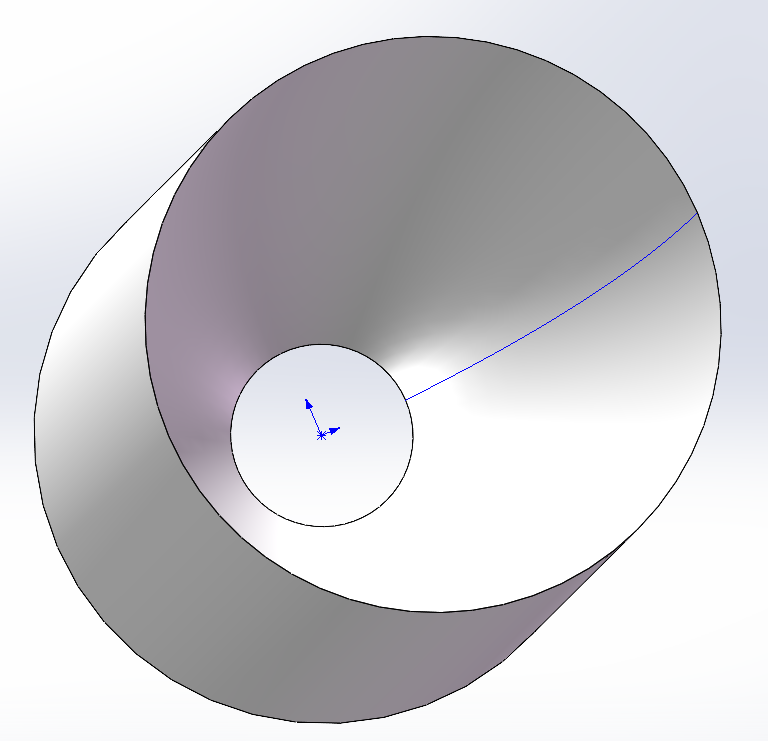
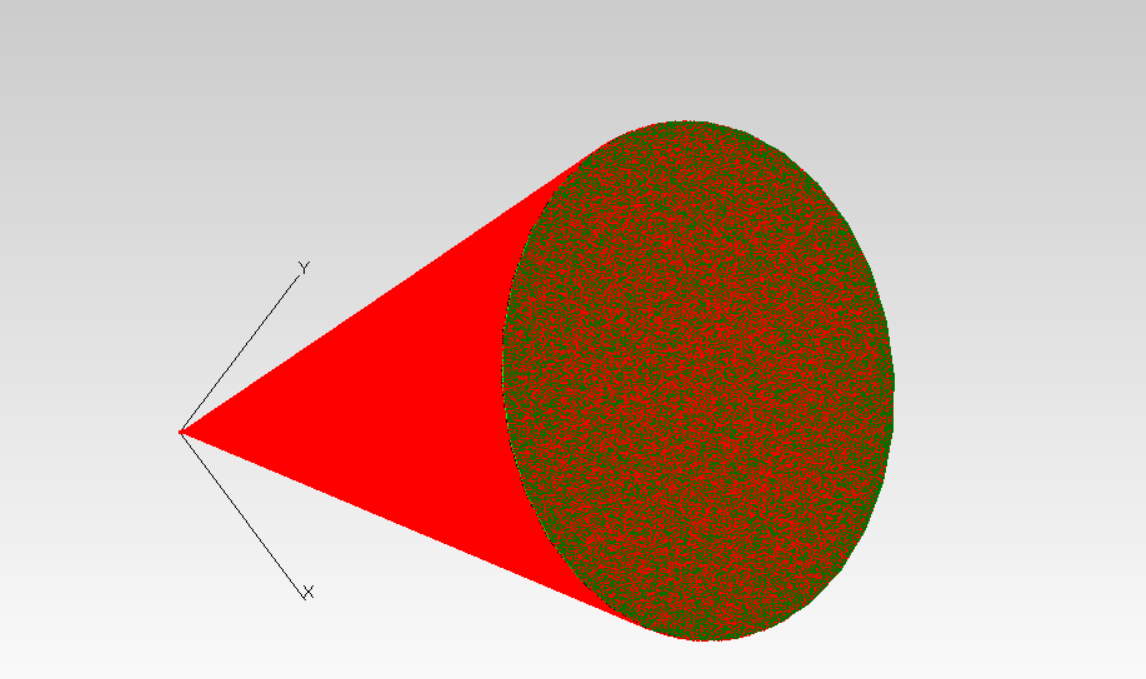
所以确定配光器的为旋转抛物面。为了使得LED 发出的光能够打到两米外，形成直径为3米的亮斑，如图1所示

基于如上外形的配光器，为了使得发射面能够在一天内吸收更多的光，需要确定合适的抛物线的参数。

CPC集光器的参数确定

该集光器是由单边的抛物线旋转得来的，所以要确定最有的集光器的外形尺寸，就需要确定抛物线，即母线。

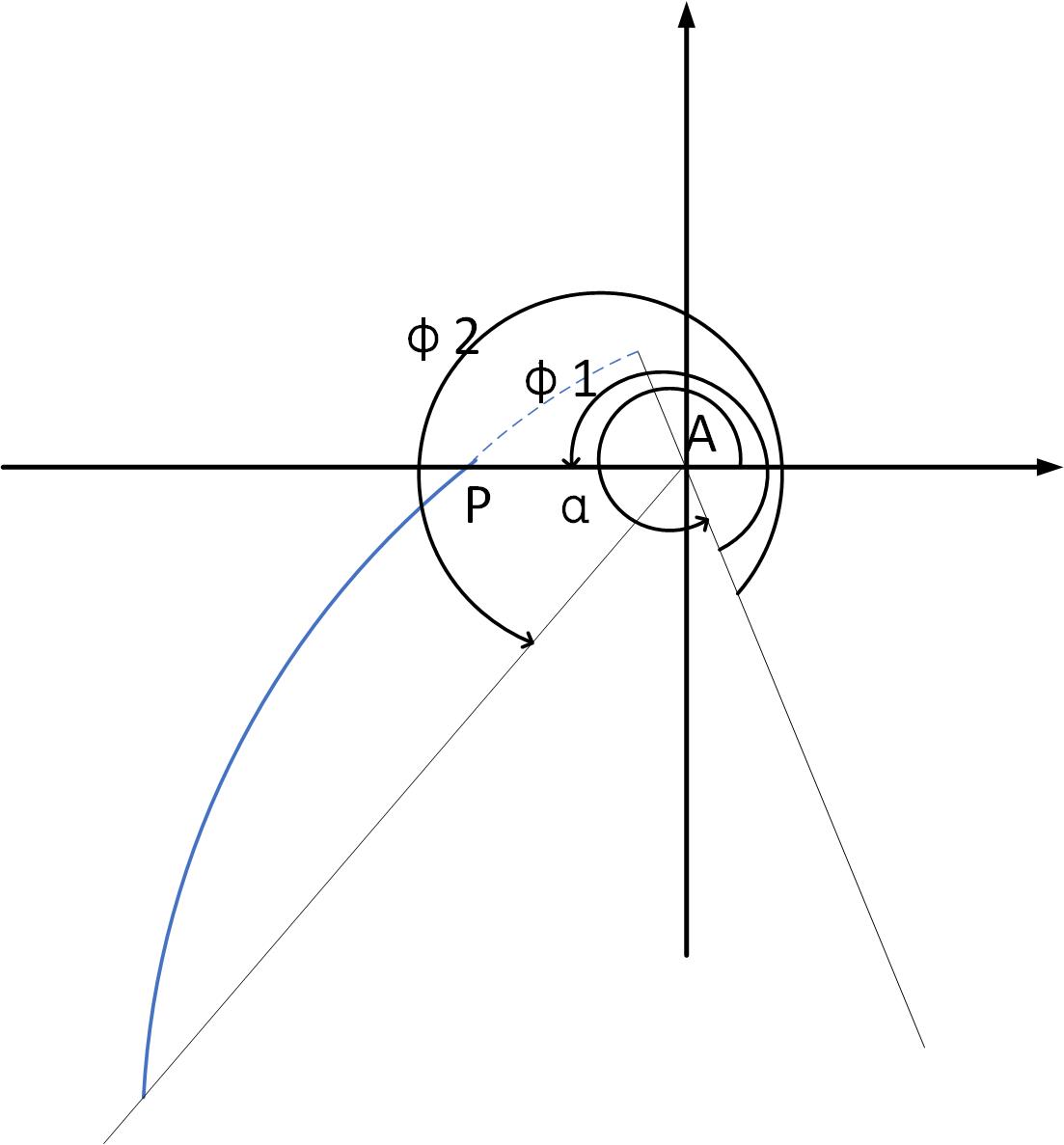
从标准的抛物线方程，可以推导出任意位置，任意开口方向的抛物线上的弧线。公式[equation1]， \[\left[\begin{array}{l} X_{1 p} \\ X_{2 p} \end{array}\right]=\frac{\sqrt{(\vec{P}-\vec{F}) \cdot(\vec{P}-\vec{F})}-(\vec{P}-\vec{F}) \cdot(\cos \alpha, \sin \alpha)}{1-\cos \phi}\left[\begin{array}{c} \cos (\alpha+\phi) \\ \sin (\alpha+\phi) \end{array}\right]+\left[\begin{array}{l} F_{1} \\ F_{2} \end{array}\right] \label{equation1}\] \(P\)表示抛物线上的一点，\(F\)表示抛物线的焦点，\(\alpha\)表示抛物线对称轴的开口方向，\(\theta\)表示抛物线的某点与焦点的连线与抛物线对称轴的夹角。

参数化的抛物线对应的图像如图2所示

焦点及所经过的点

根据边光原理，要使得入射的平行光，经抛物面反射后，落入发射面，所以可以认为焦点几位发射面上边缘的一点。又抛物面要与发射面契合，这样才能防止部分中心的光漏掉，所以可以确定抛物线经过发射面上边缘的一点\(P\)。抛物线的焦点即为抛物线经过的点\(P\) 对应的发射面的直径的另外一段,记为点\(F\)。

抛物线开口角度\(\alpha\) 的确定

为了能够保证抛物面能够将发射面发射的光能够刚好投射到两米外，形成直径为3米的光斑。如图1 所示，左半边抛物线与LED的交点与右半边抛物线的最下面的点所确定的直线与接收面的交点是光斑的边缘处。同理，右半边抛物线与LED的交点与左半边抛物线的最下面的点所确定的直线与接收面的交点也是光斑的边缘处。为了使得LED发射的光尽可能在反射一次就投射到接收面上，所以需要左（右）边抛物线的对称轴过右（左）边抛物线的最下面的点。考虑到LED的大小只有5毫米，而接收面距离LED2米，且光在接收面形成直径为3米的圆。所以可以认为左（右）边抛物线与LED的交点与右（左）边抛物线最下面的点所确定的直线与LED所在平面的夹角近似等于右(左)边抛物线与LED 的交点与右（左）边抛物线所确定的直线与LED所在平面的夹角。又由于LED尺寸太小，所以抛物线的开口方向\(\alpha\)(在实际计算时，将抛物线向上翻折，所以公式[eq:1] 所计算得到的\(\alpha\) 与程序里面用到的\(\alpha\)相差\(\pi\),后面所有的角度在计算式都如此，所以后面不在说明)可以由以下公式得出 \[\alpha=\arctan(H/D \times 2)+1.5\pi \label{eq:1}\]

其中\(H\)表示LED与接收面之间的距离，即2米。\(D\)表示接收面上光斑的直径，即3米。

抛物线范围\(\theta\) 的确定

如图3,根据抛物线的开口方向\(\alpha\),可以得到\(\phi_1\)，公式如下

\[\phi_1=1.5\pi -\arctan(H/D \times 2)\]

因为LED的大小远小于H，D，所以可以认为左边抛物线的最下面的点与点A所确定的直线与y轴的负方向的夹角等于\(\arctan(H/D \times 2)\)。如图3,可以计算\(\phi_2\) \[\phi_2=\phi_1+pi/2-arctan(H/D \times 2)\]

操作步骤

、用MATLAB编程求解出该抛物线,并将数据保存为txt文件。

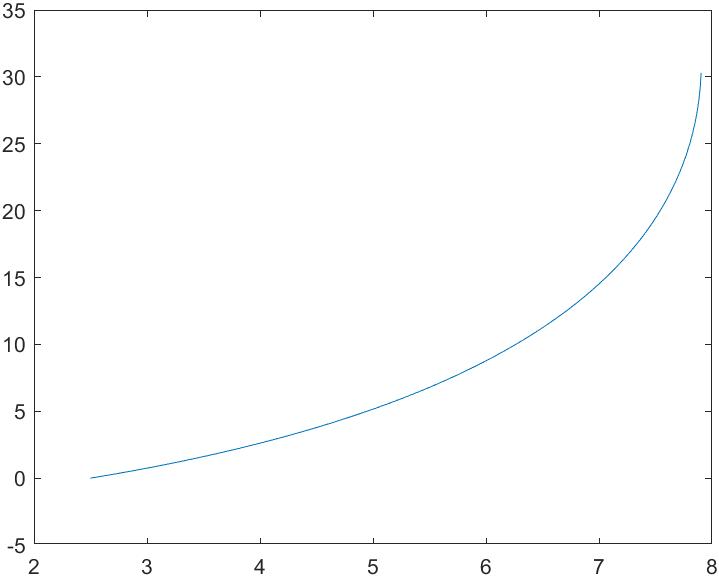
MATLAB 的具体代码见附录，所得到的抛物线(在实际编写matlab代码时，为了方便，就将抛物面向上翻转了)如下图4 所示

、将上一步所得到的抛物线导入到solidworks中，进行三维建模，得到三维的配光器。将三维模型保存为sat文件。

通过 xyz 插入曲线的方法将得到的 txt 文件中的坐标值导入，得到一条近似的抛物线，将其实体化。再插入一个圆柱体，该圆柱体。再将抛物线的两个端点与z轴做垂线，并连接两个垂直点，得到闭合的二维草图。再将该二维草图旋转切除，即可得到所需要的配光器，如下图5 的抛物面曲面。

、将sat文件导入到TracePro，添加发射面，以及光源，设置抛物面，发射面，光源的属性(是否反射，是否吸收)。设置LED(发光面）为朗泊光源光源的光通量为100 流明。配光器旋转抛物面为完全反射，设置接收面为完全吸收。

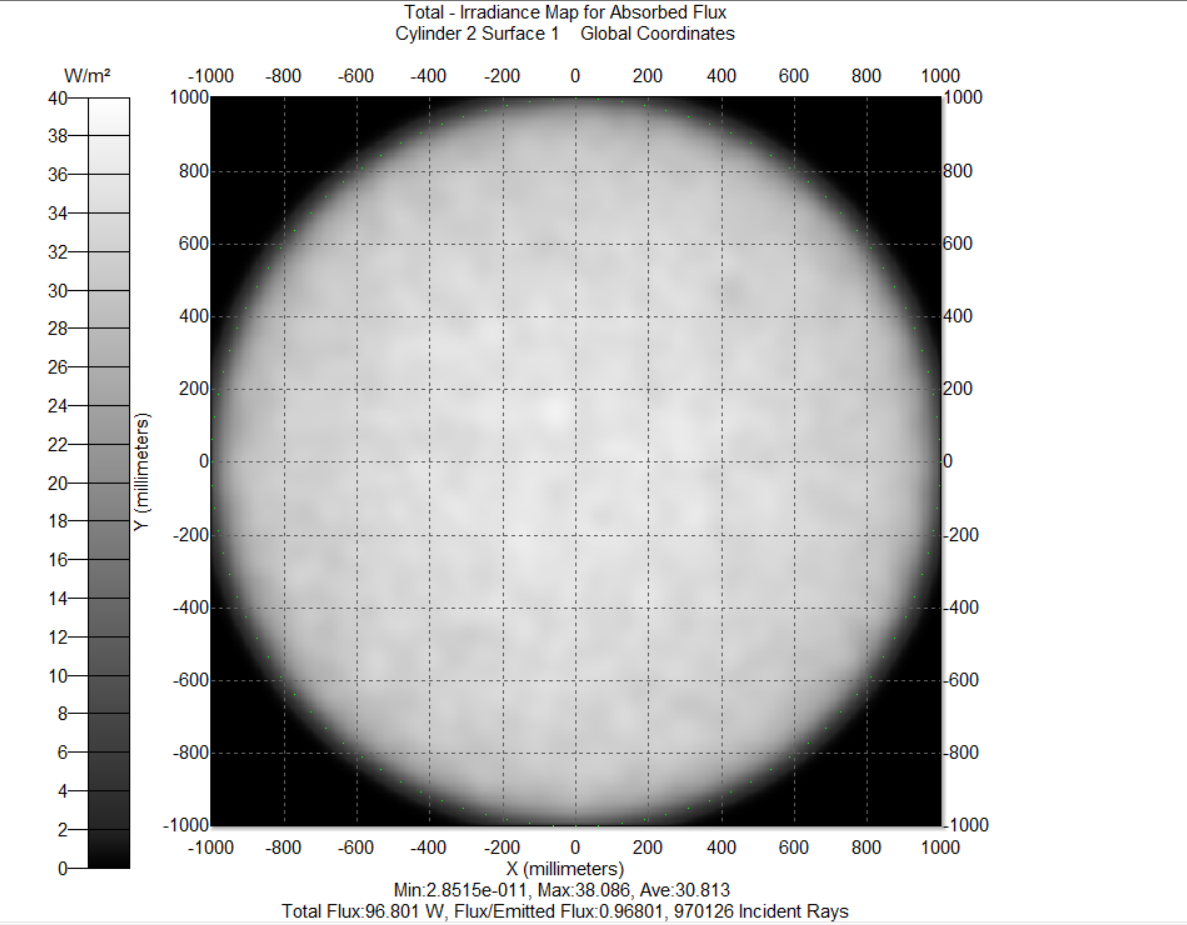
如图7,光主要分布在发射面的下半部分，且接收到的光通量为96.75w。

根据集光器的接收效率公式 \[\text{接受率}=\frac{\text{被接收器接收的光线数量}}{\text{进入CPC的光线数量}}\]

根据图6,可以发现，由于在确定抛物线开口方向\(\alpha\)，以及两个临界角\(\phi_1\),\(\phi_2\)取近似，所以实际的光斑直径略大于3米。

反思与总结

抛物流线的配光器的设计与抛物流线的集光器十分类似，仅是抛物线参数的不同。在本次实验时，在三维建模的过程中，先建立了三维的圆柱体，再根据旋转切除，得到了三维的配光器，而不仅仅是面。该操作加深了我对solid works的认识，也更熟练的操作solid works。

在MATLAB编程中，抛物线函数的编写没有使用for循环，而是尽可能的利用了MATLAB强大的矩阵计算特点，减少了代码量，也加快了代码的运行速度。

肖丽仙,何永泰.复合抛物面聚光器(CPC)在光伏/热太阳能系统中的应用及实验[J].太阳能学报,2018,39(09):2536-2543.

抛物线函数

language

function y= parabolia(f,p ,alpha,phi1,phi2)
%f,抛物线的焦点
%p抛物线上的一点
%aloha开口方向
%phi1，phi2，角度的区间
phi=[phi1:0.01:phi2];
phi=phi';
m=[cos(phi+alpha),sin(phi+alpha)];

y1=(sqrt(   (f-p)*(f-p)')  -(p-f)*[cos(alpha ),sin(alpha)]' )./(1-cos(phi));
y=y1.*m+f;

主程序

language

clear
clc
close
path="E:\文件资料\课程课件及相关资料\光学设计及光学制造\cpc配光器\CPC_配光器.jpg";
%5 mm 的led光源宽度
d=5;
%D 目标面的直径
D=2000;
%H：led与目标面的距离
H=3000;
%f：抛物线的焦点
f = [-d/2,0];
%抛物线线上的一点
p = [d/2,0];
  
%抛物线三个参数的计算  
%alpha 抛物线开口方向
alpha=pi-atan(H/D*2);
%抛物线的左半边角度限制
ph1=atan(H/D*2)+pi;
%ph2 抛物线的右半边角度的限制
ph2=2*atan(H/D*2)+pi;
%抛物线母线方程 函数 parabolia（）
y=parabolia(f,p,alpha,ph1,ph2);
plot(y(:,1)',y(:,2)');
exportgraphics(gca,path);
temp1=[y(:,1),zeros(size(y(:,1) ,1),1),y(:,2)];
save cpc_data2.txt temp1 -ascii